Zweiseitiger Signifikanztest
Inhaltsverzeichnis
\(\\\)
Aufgabenstellung
Ein Tulpenzüchter hat eine rotblühende Tulpensorte. Durch neue Züchtungsversuche hat er es erreicht, dass diese resistenter gegen Schädlingsbefall sind. Ein ambitionierter Mitarbeiter weiß, dass in \(70\%\) aller Fälle eine Blüte dieser Sorte fünf Blütenblätter hat. Durch die neue Züchtung glaubt er, habe sich dieser Anteil verändert.
Der Mitarbeiter möchte dies überprüfen und setzt dafür \(50\) Tulpenzwiebeln. Führe einen Signifikanztest durch, um die Annahme des Mitarbeiters auf einem Signifikanzniveau von \(15\%\) zu stützen.
\(\\[2em]\)
Variablendeklaration
\(x\) beschreibt die Anzahl der Tulpen mit fünf Blütenblättern und ist ist binomialverteilt mit \(n=50\).
\(\\[2em]\)
Hypothesen formulieren
Der Mitarbeiter vermutet, dass jetzt nicht mehr \(70\%\) der Tulpen fünf Blütenblätter haben. Wie viel Prozent es sind, kann er jedoch nicht sagen. Dagegen wissen wir, dass es bisher \(70\%\) war. Davon können wir auf der Basis des Signifikanzniveaus den Annahme- und Verwerfungsbereich bestimmen. Wir wählen in Übereinstimmung mit dem Prinzip des Hypothesentests diese Hypothese als Nullhypothese.
Es ergeben sich damit die Hypothesen
\( \quad \begin{array}{ r l } h_0: & p = 0{,}70 \\[5pt] h_1: & p \not= 0{,}70 \\ \end{array} \)
\(\\\)
\(h_1\) bildet die Gegenhypothese der Nullhypothese.
\(\\[2em]\)
Verwerfungsbereich der Nullhypothese festlegen
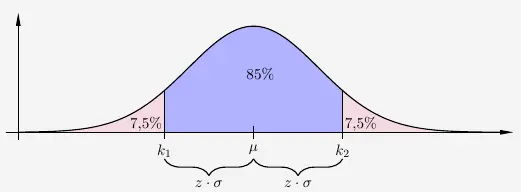
Wir arbeiten mit der Nullhypothese. Graphisch stellt es sich für die Nullhypothese wie folgt dar:

\(\\\)
Der Verwerfungsbereich ist aufgeteilt zu gleichen Teilen nach links und rechts mit jeweils der Hälfte des Signifikanzniveaus.
Es ergibt sich damit
\( \quad \begin{array}{ r c l } V & = & \{ 0 \, , \, \cdots \, , \, k_1 \} \, \cup \, \{ k_2 \, , \, \cdots \, , \, 50 \} \\[5pt] A & = & \{ k_1+1 \, , \, \cdots \, , \, k_2-1 \} \\ \end{array} \)
\(\\[2em]\)
Stelle k ermitteln
Die Stellen \(k\) werden durch die Näherung mit der Normalverteilung ermittelt.
\(\\\)


\(\\\)
Die Stelle \(k_1\) und \(k_2\) sind den Verwerfungsbereichen zugeordnet.
Gegeben sind die Werte
\( \quad \begin{array}{ r c l } n & = & 50 \\[4pt] p & = & 0{,}7 \\[4pt] \alpha & = & 0{,}15 \\ \end{array} \)
\(\\\)
Zur Berechnung benötigen wir den Erwartungswert mit
\( \quad \mu \, = \, n \cdot p \, = \, 50 \cdot 0{,}7 \, = \, 35 \)
\(\\\)
und die Standardabweichung mit
\( \quad \sigma \, = \, \sqrt{n \cdot p \cdot (1-p)} \, = \, \sqrt{50 \cdot 0{,}7 \cdot (1-0{,}7)} \, = \, 3{,}24 \, > \, 3 \)
\(\\[1em]\)
Berechnung mit dem Taschenrechner
Am Einfachsten ist die Berechnung mit dem Taschenrechner. Hier kann über die inverse Normalverteilung direkt berechnet werden für \(k_1\) mit
\( \quad \begin{array}{ r c l } \text{Fläche} & = & 0{,}075 \\[4pt] \sigma & = & 3{,}24 \\[4pt] \mu & = & 35 \\ \end{array} \)
\(\\\)
und \(k_2\) mit
\( \quad \begin{array}{ r c l } \text{Fläche} & = & 0{,}925 \\[3pt] \sigma & = & 3{,}24 \\[3pt] \mu & = & 35 \\ \end{array} \)
\(\\\)
Wir erhalten \(k_1\) mit
\( \quad \begin{array}{ r c l l } k_1 + 0{,}5 & = & 30{,}34 & | \, -0{,}5 \\[4pt] k_1 & = & 29{,}84 \\ \end{array} \)
\(\\\)
und \(k_2\) mit
\( \quad \begin{array}{ r c l l } k_2 - 0{,}5 & = & 39{,}66 & | \, +0{,}5 \\[4pt] k_2 & = & 40{,}16 \\ \end{array} \)
\(\\\)
Daraus resultiert der Verwerfungs- und Annahmebereich
\( \quad \begin{array}{ r c l } V & = & \{ 0 \, , \, \cdots \, , \, 30 \} \, \cup \, \{ 40 \, , \, \cdots \, , \, 50 \} \\[5pt] A & = & \{ 31 \, , \, \cdots \, , \, 39 \} \\ \end{array} \)
\(\\[1em]\)
Berechnung mit der Sigma-Umgebung
sind laut Aufgabenstellung gegeben. Mit der \(\sigma\)-Umgebung können die Werte für \(k\) ermittelt werden.
\(\\\)
\(\\\)
Beim Rechnen mit \(\sigma\)-Umgebung wird in der Regel auf die Stetigkeitskorrektur verzichtet. Es gilt
\( \quad \begin{array}{ r c l } k_1 & = & \mu - z \cdot \sigma \\[5pt] k_2 & = & \mu + z \cdot \sigma \\ \end{array} \)
\(\\\)
Wir benötigen zur Berechnung also \(\mu\), \(\sigma\) und \(z\) und erhalten den Erwartungswert mit
\( \quad \mu \, = \, n \cdot p \, = \, 50 \cdot 0{,}7 \, = \, 35 \)
\(\\\)
und die Standardabweichung mit
\( \quad \sigma \, = \, \sqrt{n \cdot p \cdot (1-p)} \, = \, \sqrt{50 \cdot 0{,}7 \cdot (1-0{,}7)} \, = \, 3{,}24 \, > \, 3 \)
\(\\\)
Mit dem Ansatz
\( \quad P(x \geq k_2) \, \geq \, 0{,}075 + 0{,}85 \, = \, 0{,}925 \)
\(\\\)
können wir \(z\) ermitteln mit der Tabelle für die Normalverteilung. Wir lesen
\( \quad z \, = \, 1{,}44 \)
\(\\\)
ab.
Damit ergeben sich
\( \quad \begin{array}{ r c c c l } k_1 & = & 30 - 1{,}44 \cdot 3{,}24 & = & 25{,}33 \\[5pt] k_2 & = & 30 + 1{,}44 \cdot 3{,}24 & = & 34{,}66 \\ \end{array} \)
\(\\[2em]\)
Entscheidungsregel aufstellen
Daraus ergibt sich Verwerfungs-und Annahmebereich der Nullhypothese.
\( \quad \begin{array}{ r c l } V & = & \{ 0 \, , \, \cdots \, , \, 25 \} \, \cup \, \{ 35 \, , \, \cdots \, , \, 50 \} \\[5pt] A & = & \{ 26 \, , \, \cdots \, , \, 34 \} \\ \end{array} \)
Der Verwerfungsbereich der Nullhypothese ist gleichzeitig der Annahmebereich der \(h_1\)-Hypothese. Damit ist die
\(\\\)
Entscheidungsregel:
Haben wir bei der Stichprobe von \(50\) Tulpenzwiebeln höchstens \(25\) oder mindestens \(35\) Tulpen, die fünf Blütenblätter haben, so kann die Vermutung des Mitarbeiters gestützt werden.
\(\\[2em]\)
Fehler 2. Art
Beim Fehler 2. Art tritt die Abweichung in der Regel nur zu einer der beiden Seiten auf.
Es hat sich nun heraus gestellt, dass \(80\%\) der Tulpen nach den Züchtungsversuchen fünf Blütenblätter haben. Wie lautet der \(beta\)-Fehler
An der gleichen Grenze \(k\) wird nun der Verwerfungsbereich von \(h_1\) berechnet.

\(\\\)
\( \quad \begin{array}{ r c l } \beta & = & P_{50 \, ; \, 0{,}8}(x < 35) \\[5pt] & = & P_{50 \, ; \, 0{,}8}(x \leq 34) \\[5pt] & = & 0{,}0308 \\[5pt] & = & 3{,}08 \% \\ \end{array} \)
\(\\[2em]\)